Uji Validitas dan Reliabilitas Kuesioner Menggunakan SPSS

Biasanya seorang peneliti untuk memperoleh data penelitiannya diperlukan suatu alat pengumpul data atau disebut dengan instrumen penelitian, intrumen penelitian tersebut bermacam-macam, ada yang berupa rencana pelaksanaan pembelajaran (RPP), ada juga berupa angket atau kuesioner yang isinya butir pertanyaan yang dapat dijawab oleh responden. Jadi sebelum angket atau kuesioner tersebut dibagikan ke responden, terlebih dulu di uji validitas dan reliabilitas kuesioner.

Korelasi Parsial Menggunakan SPSS

Korelasi dapat diartikan sebagai ukuran keeratan hubungan antar variabel. Dalam hal ini, untuk mengetahui keeratan satu variabel dengan variabel lainnya kita harus menggunakan paling tidak mempunyai satu variabel sebagai prediktor (independent atau bebes) yaitu variabel yang mempengaruhi atau menjelaskan terjadinya variabel lainnya dan satu lagi variabel prediktan (dependent atau terikat) yaitu variabel yang dipengaruhi atau tergantung oleh variabel lainnya

Uji Chi-Square Menggunakan SPSS

Chi-Square atau uji keselarasan merupakan salah satu uji yang paling sering digunakan dalam menganalisis data berskala nominal, bertujuan untuk menguji signifikan pada suatu sampel, uji homogenitas, uji independent dan uji goodness of fit tes.

Uji Korelasi Gamma Menggunakan SPSS

Korelasi gamma merupakan salah satu pengukuran yang termasuk ke dalam statistik nonparametrik, tujuannya mencari kekuatan dan arah hubungan yang simetris dari asosiasi yang sesuai dan cocok digunakan untuk dua variabel yang di ukur pada data skala ordinal atau variabel nominal dikotomis.  Skala yang digunakan dapat bervariasi mulai dari 0,0 sampai dengan + atau - 1,0 yang berindikasi kekuatan hubungan antara dua variabel. 

Regresi Linear Sederhana Menggunakan SPSS

Persamaan regresi adalah persamaan matematik yang memungkinkan kita meramalkan nilai-nilai suatu peubah bebas (variabel prediktor) dan peubah tak bebas (variabel respon). Istilah dari regresi itu sendiri diterapkan pada semua jenis peramalan dan tidak harus berimplikasi suatu regresi mendekati dari nilai tengah populasi. Analisis regresi digunakan terutama untuk membicarakan masalah pendugaan atau peramalan, oleh karena itu pendugaan nilai peubah variabel tak bebas Y berdasarkan peubah bebas X yang telah diketahui nilainya. 

Misalnya: untuk fenomena yang meliputi hasil panen padi dan volume pupuk yang digunakan oleh petani, dalam hal ini kita dapat menentukan variabel bebas X = volume pupuk dan variabel tak bebas Y = hasil panen. Jadi peramalan hasil panen sangat tergantung dari volume pupuk yang digunakan. 

Contoh lain, Seorang guru ingin meramalkan nilai prestasi belajar siswa tingkat persiapan pada suatu pokok bahasan, untuk membuat peramalan semacam ini, pertama-tama kita perhatikan dulu sebaran nilai pada materi yang pernah diperoleh siswa pada tahun sebelumnya, kemudian kita melambangkan nilai seseorang siswa dengan variabel tak bebas Y dan nilai prestasi belajar siswa kita lambangkan dengan variabel bebas X. Setelah di dapat nilai variabel tak bebas Y dan variabel bebas X, kemudian data tersebut dapat kita tebarkan dalam bentuk diagram pencar, dengan mengamati diagram pencar terlihat bahwa titik-titiknya mengikuti suatu garis lurus yang menunjukkan kedua peubah X dan Y saling berhubungan secara linear yang ditunjukkan seperti gambar berikut:

Dalam hal ini kita dapat menyatakan secara matematik dengan sebuah persamaan garis lurus yang disebut garis regresi linear. Sebuah garis lurus dapat ditulis dalam bentuk:

Y = a + bx

Dari persamaan garis di atas dalam hal ini Y digunakan untuk membedakan antara nilai ramalan yang didapat dari garis regresi dan nilai pengamatan Y yang sesungguhnya untuk nilai x tertentu, sedangkan a dapat dinyatakan sebagai intercept atau perpotongan dengan sumbu tegak, dan b itu kemiringan garis yang dikalikan dengan nilai x lalu ditambahkan dengan nilai a yang bertujuan untuk meramalkan nilai Y yang berpadanan pada suatu nilai x tertentu.

Sebelum kita mengaplikasikan dengan SPSS, hal yang harus kita ketahui bahwa regresi linear itu sendiri dibagi menjadi beberapa bagian, yaitu yang pertama regresi linear sederhana atau yang dikenal dengan regresi linear hanya ada satu variabel bebas (independent), yang kedua regresi linear berganda yaitu regresi linear yang lebih dari satu variabel bebas (independent) dan masih ada yang lain yang tidak disebutkan di sini, itu nanti kita bahas di artikel yang lain. Namun pada artikel kali ini kita akan mengaplikasikan kasus regresi linear sederhana menggunakan SPSS.

Contoh:
PT. Ubey Motor dalam beberapa bulan terakhir ini mengalami penurunan penjualan secara drastis terhadap motor jenis A, oleh sebab itu kepala pemasaran melakukan terobosan baru dengan cara memberlakukan promosi khusus dengan harapan dapat meningkatkan daya beli masyarakat. Promosi dilakukan pada 20 cabang yang tersebar di provinsi Aceh. Berikut data total penjualan dan biaya promosi yang dikeluarkan pada 20 cabang PT Ubey Motor tersebut.

Data di atas merupakan hasil penjualan dalam satu bulan terakhir setelah melakukan promosi. Kemudian kepala pemasaran PT tersebut ingin mengetahui seberapa jauh biaya promosi berpengaruh terhadap penjualan atau seberapa besar hubungannya. Oleh karena itu dalam hal ini kita akan menggunakanj uji regresi sederhana, karena hanya ada satu variabel bebas (independent) yaitu promosi dan satu variabel terikat (dependent) yaitu penjualan.

Berikut langkah-langkah menggunakan SPSS
1. Buka aplikasi SPSS yang telah di install sebelumnya sampai muncul area kerja berikut

2. Pada pojok kiri bawah dari gambar di atas klik Variable View dan buat variabel dari data seperti gambar berikut:

3. Bila sudah di isi semua variable view seperti gambar di atas, selanjutnya klik Data View ada pada sebelah kiri Variable view untuk kita isi data kabupaten, hasil penjualan dan biaya promosi seperti gambar berikut:

4. Selanjutnya pilih menu Analyze --- > Regression ---> Linear. bila sudah maka terlihat seperti gambar berikut:

5. Pindahkan variabel Hasil Penjualan [Penjualan] ke dalam kotak Dependent
6. Pindahkan variabel Biaya Promosi [Promosi] ke dalam kotak Independet
7. Pindahkan variabel Kabupaten ke dalam kotak Case Labels
8. jika sudah terlihat seperti gambar berikut:

9. Selanjutnya klik Options (biasa sudah terisi secara default) bila belum dapat di isi seperti berikut:

10. Dari gambar di atas dapat kita ketahui bahwa pada kotak Stepping Method Criteria kita menggunakan uji F dengan taraf kepercayaan 5% atau nilai probabilitas 0.05 yang terdapat pada kotak Entry. Biarkan secara default yaitu include constant in equation. Pada kotak Missing Values biarkan secara default yaitu Exclude cases listwise kegunaannya untuk penanganan missing value atau tidak ada data yang hilang. Selanjtnya klik Continue maka akan kembali ke gambar seperti pada langkah 8

11. Selanjtnya klik Statistik, lalu centang apa yang terlihat seperti pada bambar berikut:

12. Dari gambar di atas, pada kotak Regression Coefficients biasanya secara default sudah tercentang Estimates, karena ini perlakuan koefesien regresi untuk mengestimasi variabel. sedangkan centang model fit berguna untuk mecocokkan model regresi, dan centang Descriptives untuk mengetahui deskriptive dari data. Pada kotak Residuals centang Casewise diagnostics dan pilih All cases yang berfungsi untuk melihat pengaruh regresi terhadap hasil penjualan dan biaya promosi dari semua kabupaten. Selanjtnya klik Continue  maka akan kembali ke gambar seperti pada langkah 8.

13. Selanjtnya klik Plot. maka muncul seperti gambar berikut:

14. Dari gambar di atas, merupakan tampilan plot dapat digunakan untuk menguji asumsi-asumsi pada regresi, seperti uji normalitas, uji linieritas, dan uji kesamaan varians dari variabel. 

Kemudian klik SDRESID lalu pindahkan ke dalam kotak Y, kemudian klik ZPRED lalu pindahkan ke dalam kotak X. Jika kedua variabel tersebut sudah dimasukkan kedalam kotak Y dan kotak X, selanjtnya klik tombol Next untuk kita mengisi plot yang kedua. 

Pertama kota tersebut terlihat kosong seperti semula, sekarang pilih ZPRED lalu masukkan kedalam kotak Y, kemudian klik DEPENDNT lalu pindahkan ke dalam kotak X, selanjutnya klik tombol Next untuk kita mengisi plot yang ketiga.

untuk plot yang ketiga pada bagian Standarized Residual Plots cukup centang Normal probability plot saja seperti terlihat pada gambar berikut:

15. Selanjutnya klik Continue dan tekan OK.

ANALISIS
Bagian Output Descriptive Statistics dan Correlation

Analisis bagian Descriptive Statistics

• Rata-rata hasil penjualan PT ubey motor dari 20 cabang yang ada di Provinsi Aceh adalah Rp. 307.40 juta dengan standar deviasi Rp. 20.332 juta.

• Rata-rata biaya promosi PT ubey motor dari 20 cabang adalah Rp. 28.80 juta dengan standar deviasi Rp. 3.334 juta

Analisis bagian Correlations

• Besar hubungan antara hasil penjualan dengan biaya promosi dapat diketahui dengan melihat koefesien korelasi adalah 0.740. artinya nilai ini dapat menunjukkan hubungan yang sangat kuat antara hasil penjualan dengan biaya promosi, nilai koefesien korelasi semakin mendekati ke 1 maka semakin sempurna hubungan antara kedua variabel tersebut (arah hubungan ke positif).

• Taraf kepercayan yang digunakan yaitu 0.05. diperoleh hasil tingkat signifikan koefesien korelasi sebesar 0.071. karena nilainya lebih besar dari 0.05 maka hubungan hasil penjualan dengan biaya promosi tidak berbeda secara nyata.

Analisis bagian Variables Entered dan Model Summary

Analisis bagian Variabel Entered/Removed
Tabel tersebut diperlihatkan bahwa variabel yang kita masukkan yaitu biaya promosi dan tidak terdapat variabel yang dikeluarkan (removed). karena metode yang kita pakai adalah single step

Analisis bagian Model Summary
Pada tabel model tersebut dapat diketahui bahwa nilai R sebesar 0.740 atau koefesien korelasi nilai R tersebut dapat dikuadratkan yaitu 0.740 x 0.740 = 0.548. R square (koefesien determinasi) dalam hal ini variasi dari variabel terikat (hasil penjualan) dapat dijelaskan oleh variabel bebas (biaya promosi) yaitu sebesar 54.8%. sedangkan sisanya 45.2% dipengaruhi oleh faktor yang lain. Tingkat besarnya hubungan dari kedua varibabel tersebut dapat dilihat pada tabel berikut:

Dari tabel diatas dapat diketahui bahwa hubungannya kuat antara hasil penjualan dengan biaya promosi.

Standard Error of the Estimate sebesar 15.636 dapat diartikan bahwa hasil penjualan yang dipakai dari variabel terikat sebesar Rp.15.636 juta. sedangkan bila kita lihat pada tabel sebelumnya (tabel descriptive statistics) nilai standar deviasi hasil penjualan diperoleh sebesar Rp. 20.322 juta, nilai ini mendandakan standar error of the estimate lebih besar dari pada yang diperoleh dari  model hanya Rp.15.636 juta.

Analisis bagian Anova dan Coefficients

Analisis bagian Anova
Dari tabel uji anova diperoleh nilai F tes (F hitung=51.352) dan nilai probabilitas (signifikan) kecil dari 0.05. karena nilai probabilitas kecil dari 0.05 maka model regresi ini dapat digunakan untuk memprediksi hasil penjualan.

Analisis bagian Coeffecients
Pada bagian ini kita akan memperoleh persamaan regresi yaitu:
Y = 247.727 + 2.072X
keterangan:
Y = hasil penjualan
X = biaya promosi
Dari persamaan di atas nilai 247.727 merupakan konstanta, artinya bila tidak ada biaya promosi (x) maka hasil penjualan tetap sebesar 247.727 juta.
koefesien regresi 2.072 menandakan setiap ada peningkatan satu satuan (x=biaya promosi) maka Y ada peningkatan satu-satuan tergantung nilai x, begitu juga sebaliknya.

Dalam hal ini uji t sangat dibutuhkan untuk menguji signifikan konstanta dan varibel bebas (biaya promosi). Persamaan regresi yang telah diperoleh sebelumnya akan di uji apakah variabel bebas (biaya promosi) dapat dijadikan sebagai variabel untuk memprediksi hasil penjualan yang akan datang.

Sebelumnya kita buat hipotesis:
H0 = koefesien regresi tidak signifikan
H1 = koefesien regresi signifikan

Pengujian statistik:
jika t hitung < t tabel maka H0 diterima, nilai probabilitas > 0.05
jika t hitung > t tabel maka H1 di tolak, nilai probabilitas < 0.05

dari hasil perhitungan diperoleh nilai t hitung 6.326 dan t tabel 1.73. jadi 6.326 > 1.73. dan nilai signifikan atau probabilitas 0.00. maka berdasarkan pengujian statistik H0 di tolak dan terima H1. Jadi koefesien regresi signifikan atau biaya promosi berpengaruh secara nyata terhadap hasil penjualan.

Kesimpulan:
Berdasarkan hasil perhitungan di atas model regresi yang diperoleh sebelumnya dapat dijadikan sebagai alat untuk memprediksi hasil penjualan yang akan datang.

Uji Marginal Homogenity Menggunakan SPSS

Uji Marginal Homogenity ini sebenarnya masih dalam satu paket Uji McNemar, cuma bedanya pada skala data yang digunakan, artinya bila skala datanya nominal (dikotomi) maka gunakanlah uji McNemar kunjungi pada alamat: Uji McNemar menggunakan SPSS. Sedangkan untuk skala data ordinal seperti ("suka", "kurang suka", "tidak suka") atau ("puas", "kurang puas", "tidak puas") atau dengan kata lain yang lebih dari 2 pilihan, untuk itu kita menggunakan Uji Marginal Homogenity. itu semua termasuk kedalam statistik nonparametrik.

Uji McNemar Menggunakan SPSS

Uji McNemar merupakan salah satu alat statistik nonparametrik yang digunakan untuk menguji perbedaan dua sampel berpasangan (anggita sampel yang sama), bentuk skala data yang digunakan yaitu skala nominal atau dikotomi. Pada umumnya uji McNemar ini dugunakan untuk mengukur sebelum dan sesudah diberikan suatu perlakuan pada sampel tersebut, bentuk isian data hanya ada dua pilihan yaitu "Ya" atau "Tidak", "suka" atau "tidak suka", "Berminat" atau "tidak berminat" dan lain sebagainya, bentuk isiannya di berikan pengkodean dari masing-masing pemilihan yaitu 1 atau 2, contoh: 1=Ya, dan 2= tidak.

Uji Kruskall Wallis menggunakan SPSS

Uji kruskall wallis termasuk kedalam uji statistik nonparametrik yang digunakan untuk menguji lebih dari dua sampel yang bersifat bebas satu dengan yang lain dan data yang digunakan berbentuk skala nominal dan ordinal, namun uji kruskall wallis ini juga dapat digunakan untuk data skala interval dan rasio untuk uji yang lebih dari dua sampel pada statistik parametrik (uji ANOVA) manakala asumsi pada statistik parametrik tidak terpenuhi (misalnya: data tidak berdistribusi normal dan tidak homogenitas) maka alternatif lain dapat digunakan statistik nonparametrik yaitu uji kruskall wallis. 

Uji Cochran Menggunakan SPSS

Uji cochran digunakan pada pengujian statistik non-parametrik untuk sampel lebih dari 2 variabel, Uji ini mempunyai ciri tersendiri, dimana nilai yang digunakan dari suatu perlakuan hanya dinyatakan dalam 2 nilai yaitu 1=suka, 0=tidak suka, skala data yang digunakan untuk uji cochran yaitu skala nominal.

Uji Mann-Whitney Menggunakan SPSS

Uji Mann-Whitney test adalah salah satu uji statistik non-parametrik yang digunakan untuk uji sampel bebas (independent) yang berjumlah 2 sampel serta keduanya tidak saling berhubungan satu dengan yang lainnya. Uji ini mempunyai tujuan yang sama seperti uji t pada statistik parametrik, uji t untuk statistik parametrik harus memenuhi uji asumsi terlebih dahulu yaitu data harus berdistribusi normal, manakala uji asumsi distribusi normal tidak terpenuhi untuk data skala interval dan rasio, maka alternatif lain sebagai pengganti uji t bisa kita gunakan uji Mann-Whitney.

Uji Wilcoxon Menggunakan SPSS

Uji wilcoxon (uji tanda) termasuk kedalam statistik non-parametrik, data yang digunakan berupa skala nominal dan ordinal. Uji ini menggunakan dua sampel yang saling berhubungan (berpasangan) yang bertujuan untuk mengetahui apakah keduanya mempunyai hubungan. Uji wilcoxon merupakan alternatif lain dari uji t untuk data berpasangan (t-paired), pada uji wilcoxon data harus dilakukan pengurutan (ranking) sebelum di lakukan untuk pengujian. 

Uji Two Way Anova Menggunakan SPSS

Uji two way anova (uji anava dua arah) digunakan untuk pengujian statistik yang lebih dari 2 sampel, uji anava dua arah ini digunakan untuk mengetahui apakah ada interaksi antar faktor yang akan di teliti. Pada dasarnya uji ini sama dengan uji yang lain yang bertujuan sama-sama untuk mengetahui varians setiap faktor hanya saja langkah untuk menempuh hasil yang berbeda-beda tergantung banyaknya sampel dan uji statistik yang hendak dipakai. 

Uji One Way Anova Menggunakan SPSS

ANOVA (analisis of Varians) digunakan untuk pengujian statistik yang lebih dari 2 sampel, uji yang digunakan adalah uji F. Uji ANOVA dibagi 2 bagian yaitu one way anova (anova satu faktor) dan two way anova (anova dua faktor). 

Uji Normalitas Menggunakan SPSS

Uji normalitas statistik parametrik

Uji normalitas (distribusi gauss) bagi yang menggunakan statistik parametrik itu wajib, kenapa? karena agar langkah-langkah selanjutnya dapat dipertanggungjawabkan dalam pengujian hipotesis.

Uji t sampel berpasangan Menggunakan SPSS

Uji t sampel berpasangan (Statistik Parametrik)

Uji t sampel berpasangan digunakan pada saat analisis dilakukan terhadap satu sampel dengan subjek yang sama namun mengalami dua perlakuan yang berbeda, gunanya untuk mengetahui apakah ada perbedaan secara signifikan sebelum dan sesudah di berikan perlakuan, banyak anggota dalam satu sampel biasanya >= 30 untuk pengujian statistiknya (sudjana; 2005). Nilai yang diperoleh tentunya dari hasil tes pada suatu sampel. 

Cara Transformasi Data Menggunakan SPSS

Transformasi data digunakan pada saat dimana data hasil uji normalitas tidak normal. Peneliti yang hendak menguji normalitas data banyak yang menggunakan cara analitis untuk melihat distribusi sampel berdistribusi normal atau tidak yaitu menggunakan uji koolmogorv-smirnov dan shapiro-wilk tergantung banyak anggota sampelnya. Mungkin beberapa ahli statistik mereka cenderung melihat distribusi data statistik deskriptifnya yaitu nilai kurtosis, nilai skewnes, varians, plot histrogram dan lain sebagainya untuk memutuskan data berdistribusi normal atau tidak. 

Uji t Sampel tidak Berpasangan Menggunakan SPSS

Uji t sampel tidak berpasangan (Statistik Parametrik)

Uji t sampel tidak berpasangan digunakan pada saat analisis dilakukan terhadap 2 sampel dengan subjek yang berbeda dan mengalami perlakuan yang berbeda, gunanya untuk mengetahui apakah ada perbedaan secara signifikan kelompok A dengan kelompok B.

Uji t Satu Sampel Menggunakan SPSS

Uji t Satu Sampel

Uji t satu sampel digunakan pada saat dimana analisis yang dilakukan terhadap satu sampel, uji satu sampel yang dimaksud disini bukanlah satu sampel berpasangan dimana kalau uji satu sampel berpasangan dilakukan terhadap satu sampel yang diberikan dua perlakuan yang berbeda terhadap sampel tersebut. Yang saya bahas dalam halaman ini hanyalah uji satu sampel untuk melihat perbedaan salah satu atau beberapa anggota dari sampel terhadap keseluruhan anggota dalam satu sampel tersebut. Uji satu sampel seperti ini peneliti pada umumnya hanya untuk menjawab pertanyaan penelitiannya seperti:

Statistik Deskriptif menggunakan SPSS

Statistik deskriptif  hanya menjelaskan karakteristik dari data baik data interval, rasio, nominal dan ordinal. Statistik deskriptif harus selalu mendahului statistik analitis dengan tujuan untuk mengetahui hal-hal penting dari sekelompok data. seperi mean (rata-rata), standar deviasi, median dan lain sebagainya.

Pengantar Statistik

Dalam kehidupan sehari-hari ilmu statistik sudah banyak digunakan yang ditampilkan dengan sederetan angka atau numeric dalam dunia programmer, contohnya gaji karyawan, nilai siswa, jumlah peserta, banyak penduduk dan lain sebagainya. dengan demikian untuk memperoleh data statistik ada 2 macam yaitu data primer (memalui survei atau hasil laboratorium) dan data sekunder (data yang diroleh secara langsung) dan terorganisir dengan cara tertentu. Hampir semua data yang kita kenal dapat dikategorikan sebagai data statistik, karena statistik sudah dipakai pada semua bidang seperti pendidikan, manajemen ekonomi, kesehatan, sosail, dan lain sebagainya.

Prinsipnya ilmu statistik dapat dibagi menjadi 2 bagian yaitu:

1. Statistik deskriptif

Statistik deskriptif hanya menjelaskan atau menggambarkan karakteristik dari data. Statistik deskriptif harus selalu mendahului statistik analitis yang tujuannya untuk menggambarkan hal-hal penting dari sekelompok data, seperti rata-rata, standar deviasi, median, modus, quartil, desil, persentil dan lain sebagainya.

2. Statistik Inferensi

Statistik inferensi atau statistik induktif berkaitan erat hubungannya dengan pengambilan keputusan dari data yang sudah di uji statistiknya. Tindakan inferensi tersebut seperti melakukan prakiraan besar populasi, uji hipotesis, prediksi, korelasi dan lain sebagainya.

Sebelum memilih uji statistik apa yang mau dipakai, baiknya kita kenali dulu pendekatan dan skala data statistik yaitu:

 

1.  Data kualitatif

Data kualitatif merupakan data yang direpresentasikan dalam bentuk uraian, kata-kata, mendeskripsikan atau analisis hasilnya. Jenis data kualitatif dibagi 2 yaitu: skala nominal dan skala ordinal.

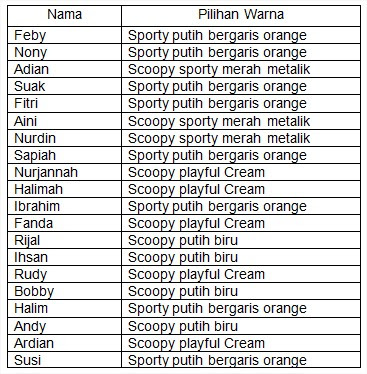
Data skala nominal merupakan hasil dari pengukuran kualitatif yang sering digunakan untuk mengidentifikasi, klasifikasi, dan membedakan objek. jenis data demikian  tidak ada tingkatannya lebih tinggi atau rendah melainkan hanya mengkategorikan saja. Misalnya: jenis kelamin (1=laki-laki, 2=perempuan), daerah (1=Aceh, 2=Medan, 3=Lampung), negara (1=Indonesia, 2=Arab, 3=Amerika), pekerjaan (1=petani, 2=PNS, 3=IRT) dan lain sebagainya.

Data skala ordinal termasuk ke dalam data pengukuran secara kualitatif, karena jenis data tersebut mempunyai karakteristik nominalnya dan memiliki tingkatan atau derajatnya. Misalnya: (1=tidak suka, 2=suka, 3= cukup suka, 4= sangat suka), pangkat atau golongan (1=asisten ahli, 2=lektor, 3= lektor kepala, 4=guru besar), juara kelas (1=peringkat 1, 2=peringkat 2, 3=peringkat 3) dan lain sebagainya.

2. Data kuantitatif

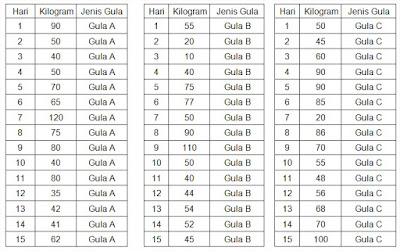
Data kuantitatif merupakan data berupa angka atau nilai. Misalnya: nilai ujian siswa, berat badan, nilai laboratorium dan lain sebagainya. Data kuantitatif dibagi menjadi 2 bagian yaitu: Data interval dan data rasio. data tersebut tidak mempunyai kategori variabel melainkan angka (numeric) yang diperoleh. Kita dapat membedakan data interval dan data rasio berdasarkan nilai 0 dalam arti yang sesungguhnya. 

Apabila data yang diperoleh tidak mempunyai nilai 0 yang sesungguhnya seperti rentang umur 10-30 bulan/tahun, rentang nilai 50-80, kecepatan mengendarai motor Anto (40 point) dua kali lebih kencang dibandingkan motor budi (20 point), jarak antara point 4 dan point 5 sama jarak dengan point 6 dan point 7 dan lain sebagainya, bentuk data ini termasuk data skala interval. 

Apabila data yang diperoleh mempunyai nilai 0 seperti nilai ujian, pendapatan, jarak tempuh dan lain sebagainya ini disebut data skala rasio.

Mengenal skala pengujian dalam ilmu statistik

Sebelum memilih teknik pengujian apa yang seharusnya digunakan dalam pengolahan data, berikut penjelasan uji statistik berdasarkan jenis data yang diperoleh

1. Statistik parametrik

Statistik parametrik adalah ilmu statistik yang mempunyai uji asumsi sebelum data tersebut digunakan untuk pengujian hipotesis. Data yang digunaka yaitu data berbentuk interval dan rasio. Uji asumsi yang dimaksud adalah uji normalitas, uji homogenitas, kolinearitas, autokorelasi dan sebagainya tergantung uji statistik yang hendak dipakai. Apabila data tidak memenuhi uji asumsi untuk statistik parametrik maka solusi lain bisa kita menggunakan statistik nonparametrik.

2. Statistik nonparametrik

Statistik nonparametrik adalah ilmu statistik yang tidak memerlukan uji asumsi apa-apa, tetapi uji ini terlalu mudah. skala yang digunakan yaitu data nominal dan data ordinal

Gambar berikut pengelompokan uji statistik parametrik dan statistik nonparametrik

Dari gambar diatas kita dapat menggunakan uji statistik berdasarkan jenis data yang diperoleh dan persyaratan uji asumsi untuk statistik parametrik. pengujian hipotesis ada dipembahasan yang lain. Semoga artikel bermanfaat buat kita semua.